苹果正在改进其屏下指纹扫描技术
本文共 524 字,大约阅读时间需要 1 分钟。
根据一份新公布的专利申请,苹果正在改进其尚未使用的屏下指纹扫描技术。
这项专利申请最早由 Patently Apple 发现,并提交给美国专利商标局,名为“基于离轴角光的屏下指纹传感”,解释了如何使屏下指纹扫描仪更准确、更可靠。苹果将其技术描述为“增强型屏下指纹传感”系统,与安卓设备上使用的许多其他现有屏下指纹扫描仪不同,该系统使用“离轴角光”在不增加部件尺寸的情况下更有效地读取指纹。
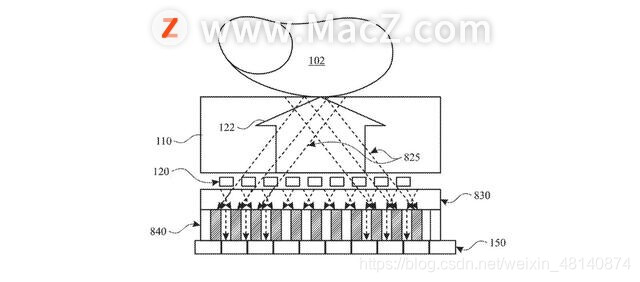
大多数光学屏下指纹扫描系统使用设备显示屏发出的光来照亮用户的指尖,通过显示像素之间的微小开口反射。然后,显示屏下方的传感器可以读取指纹并对用户进行身份验证。
由于显示屏堆叠造成的“低光吞吐量和衍射”,指纹图像容易受到低对比度和低信噪比的影响,使得指纹更难读取,并可能增加认证用户所需的时间。
为了克服这个问题,苹果提出了一种系统,通过一系列“显示屏和传感器之间的角度相关过滤选项”来捕捉来自手指的离轴角度光。据苹果公司称,这种方法可以“提高指纹印象的对比度,并保持整个传感系统的紧凑性”。
据分析师郭明錤称,苹果计划 2023 年在至少一款高端的 iPhone 上安装指纹扫描仪,但巴克莱分析师最近表示,这一功能最快可能在今年的 iPhone 13 上推出。
转载地址:http://eyzqz.baihongyu.com/
你可能感兴趣的文章
netty 主要组件+黏包半包+rpc框架+源码透析
查看>>
Netty 异步任务调度与异步线程池
查看>>
Netty中实现多客户端连接与通信-以实现聊天室群聊功能为例(附代码下载)
查看>>
Netty中集成Protobuf实现Java对象数据传递
查看>>
netty之 定长数据流处理数据粘包问题
查看>>
Netty事件注册机制深入解析
查看>>
Netty入门使用
查看>>
Netty原理分析及实战(一)-同步阻塞模型(BIO)
查看>>
Netty原理分析及实战(三)-高可用服务端搭建
查看>>
Netty原理分析及实战(四)-客户端与服务端双向通信
查看>>
Netty发送JSON格式字符串数据
查看>>
Netty和Tomcat的区别已经性能对比
查看>>
Netty基础—1.网络编程基础二
查看>>
Netty基础—2.网络编程基础四
查看>>
Netty基础—3.基础网络协议二
查看>>
Netty基础—7.Netty实现消息推送服务一
查看>>
Netty基础—7.Netty实现消息推送服务二
查看>>
Netty基础—8.Netty实现私有协议栈二
查看>>
Netty多线程 和 Redis6 多线程对比
查看>>
Netty学习总结(2)——Netty的高性能架构之道
查看>>